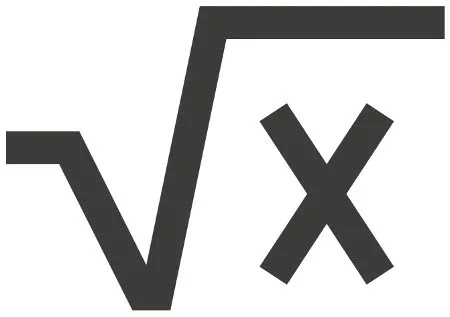Plataforma brasileira aposta em IA para ensino de português e matemática
 |
| Foto: Reprodução |
O Ecossistema de Tecnologia e Inovação lançou uma versão aprimorada de sua plataforma de ensino adaptativo, a Aprimora, versão 5.0. Essa atualização marca um avanço significativo ao introduzir inteligência artificial generativa, focada em estudantes brasileiros de matemática e português.
A Aprimora 5.0 promete trazer um ambiente educacional envolvente, colocando o aluno como o centro da experiência de aprendizagem. Utilizando elementos de gamificação, a plataforma motiva os alunos, recompensando seu progresso e oferecendo recursos de acessibilidade, como ajustes de fonte, Libras e alto contraste.
A interface da plataforma simula uma cabine de controle de submarino, onde cada ano escolar corresponde a uma ilha temática com desafios a serem enfrentados. O sucesso nessas atividades permite que os alunos personalizem suas ilhas, aumentando assim a individualização da aprendizagem.
Martin Oyanguren, CEO do Educacional, destaca que a Aprimora 5.0 visa potencializar o estudo dos alunos sem substituir a busca ativa pelo conhecimento. A plataforma está disponível como parte da Suíte Educacional, que oferece uma ampla gama de soluções educacionais em todos os níveis da educação básica.
Um dos pontos mais inovadores da Aprimora 5.0 é a integração de um chat com inteligência artificial, apelidado de "MARIA". Esse recurso auxilia os alunos na resolução de problemas, no esclarecimento de dúvidas e na adaptação do conteúdo às suas necessidades específicas.
Além disso, a plataforma oferece ferramentas aprimoradas para professores e gestores educacionais. Eles podem monitorar o progresso dos alunos de forma detalhada, utilizando novos indicadores de desempenho e engajamento para identificar áreas de melhoria e fornecer um suporte mais personalizado.
Fonte: Tudo Celular.com
Link da matéria original: https://www.tudocelular.com/tech/noticias/n217665/plataforma-brasileira-aposta-em-ia-para-ensino-de-portugues-e-matematica.html
O problema matemático que intrigava Napoleão e que se aplica em IA e no carreto da sua mudança
O maior general da história, como reconhecido por muitos especialistas, foi um homem de paixões intensas. O que talvez não seja tão conhecido é que uma delas era a ciência.
“Se eu não tivesse me tornado comandante-chefe e instrumento do destino de um grande povo, (…) teria me lançado no estudo das ciências exatas. Eu teria caminhado ao lado dos Galileus e dos Newtons.
E como tive êxito constante em meus grandes empreendimentos, também teria me destacado muito no trabalho científico. Teria deixado a memória de belas descobertas. Nenhuma outra glória teria tentado a minha ambição”, disse Napoleão Bonaparte, segundo o físico francês François Arago.
Ele não apenas amava a ciência, mas percebeu que os cientistas poderiam ajudá-lo em seu ambicioso projeto político.
Leia mais em: https://www.bbc.com/portuguese/articles/cndp02023p7o
Fonte: BBC
A Matemática Iluminando Nosso Mundo: Da Cozinha à Medicina, Uma Jornada Números
A Matemática Iluminando Nosso Mundo: Da Cozinha à Medicina, Uma Jornada Números
Na intricada teia que forma o tecido da nossa realidade, a matemática emerge como uma luz guia, proporcionando clareza e compreensão em diversos aspectos do nosso dia a dia. Dos fogões das cozinhas às salas de cirurgia da medicina moderna, e até mesmo nos gráficos que permeiam a mídia, a matemática é a linguagem universal que traduz o mundo complexo que nos rodeia.
Na Cozinha: Uma Pitada de Matemática em Cada Receita
Ao abrir o livro de receitas, nos deparamos com a dança harmoniosa dos números. Desde as proporções exatas de ingredientes até os tempos de cozimento precisos, a matemática desempenha um papel crucial na culinária. A arte da gastronomia se revela como uma equação delicada, onde a precisão das medidas é a chave para criar pratos irresistíveis.
Na Medicina: O Coração das Operações Matemáticas
Nos corredores dos hospitais, a matemática assume um papel vital na vida e na morte. Desde o cálculo de doses precisas de medicamentos até a interpretação de resultados de exames, a matemática orienta os profissionais de saúde em suas decisões cruciais. Algoritmos matemáticos avançados são a espinha dorsal das tecnologias médicas modernas, permitindo diagnósticos mais rápidos e tratamentos mais eficazes.
Na Mídia: A Narrativa dos Números
Ao folhear jornais ou assistir às notícias, somos confrontados com a influência da matemática na comunicação de informações complexas. Gráficos, estatísticas e porcentagens são as ferramentas que traduzem eventos globais em linguagem compreensível. A matemática não apenas informa, mas também molda a narrativa, dando forma à compreensão pública de questões prementes.
A Luz no Final do Túnel: O Poder Transformador da Matemática
Nossa jornada pelo mundo dos números nos revela que a matemática não é apenas uma disciplina acadêmica distante, mas sim uma presença constante e essencial em nossas vidas. Seja na cozinha, na medicina ou na mídia, a matemática nos guia, fornecendo as ferramentas para entendermos, analisarmos e prosperarmos no complexo tecido da existência humana.
Enquanto continuamos a desbravar os mistérios do universo, a matemática permanece como a luz no final do túnel, iluminando o caminho para o entendimento mais profundo do lugar que chamamos de lar.
Publicado em 17/01/2024.
Por que a tabuada do 9, todos os noves são foras?
Por exemplo, se multiplicarmos 9 por 2, o resultado é 18. A soma de seus dígitos (1 + 8) é igual a 9. Outro exemplo é 9 multiplicado por 6, que é igual a 54. A soma de seus dígitos (5 + 4) também é igual a 9.
Essa propriedade é válida para todas as multiplicações da tabuada do 9. Vamos considerar alguns casos:
- 9 x 3 = 27, cuja soma dos dígitos (2 + 7) é igual a 9.
- 9 x 4 = 36, cuja soma dos dígitos (3 + 6) é igual a 9.
- 9 x 7 = 63, cuja soma dos dígitos (6 + 3) é igual a 9.
- E assim por diante.
Essa é a razão pela qual dizemos que "todos os noves são foras" na tabuada do 9.
Aprenda de forma simples e prática a Potenciação e Radiciação
A potenciação e radiciação são operações matemáticas fundamentais que envolvem o uso de expoentes e raízes. Para aprender e entender esses conceitos, você pode seguir as seguintes etapas:
1. Entenda a definição de potenciação: A potenciação consiste em multiplicar um número por ele mesmo várias vezes. Por exemplo, 2 elevado a 3 (2³) significa multiplicar o número 2 por ele mesmo três vezes: 2 x 2 x 2 = 8.
2. Conheça as propriedades da potenciação: Existem algumas propriedades importantes da potenciação, como a propriedade da multiplicação, divisão, potência de expoente zero e potência de expoentes negativos. Estude cada uma dessas propriedades para entender como aplicá-las em diferentes situações.
3. Familiarize-se com os termos: Ao realizar uma potenciação, é importante entender os termos envolvidos. Por exemplo, a base é o número que está sendo multiplicado, e o expoente indica quantas vezes a base deve ser multiplicada por si mesma.
4. Aprenda a calcular raízes: A radiciação é a operação oposta à potenciação, e envolve encontrar a raiz de um número. Para calcular uma raiz quadrada, por exemplo, você deve encontrar o número que, quando multiplicado por si mesmo, resulte no número dado. Por exemplo, a raiz quadrada de 25 é 5, pois 5 x 5 = 25.
5. Pratique com exemplos: Resolva vários exercícios e problemas envolvendo potenciação e radiciação para ganhar mais experiência e compreensão desses conceitos. Use exemplos práticos para entender como essas operações são aplicadas no dia a dia.
Lembre-se de que a prática é fundamental para aprender e entender potenciação e radiciação.
Quanto mais você se familiarizar com os conceitos e praticar, mais confiante ficará na sua habilidade de utilizá-los em situações diferentes.
A regra de três e o conceito matemático mais utilizado no dia a dia
 |
| Photo by Clayton Robbins on Unsplash |
Para entender melhor a utilização da regra de três
Para entender melhor a utilização da regra de três, vamos considerar um exemplo prático. Suponha que um pedreiro demore 8 dias para construir um muro de determinada altura. Se ele precisa construir um segundo muro de altura igual, quanto tempo irá demorar?
Podemos usar a regra de três para resolver esse problema. Vamos chamar de "dias" a unidade de medida do tempo e de "muros" a unidade de medida da quantidade de muros construídos. Temos, então, a seguinte relação: 8 dias para 1 muro.
Podemos estabelecer a proporção entre os dois muros
A partir dessa relação, podemos estabelecer a proporção entre os dois muros. Se o segundo muro terá a mesma altura do primeiro, então podemos afirmar que são dois muros iguais. Portanto, a proporção fica da seguinte maneira: 8 dias para 1 muro, x dias para 2 muros.
Agora, basta aplicar a regra de três. Multiplicamos 8 por 2 para obter 16 dias. Portanto, o pedreiro irá demorar 16 dias para construir dois muros de altura igual ao primeiro.
Podemos estabelecer a proporção da seguinte maneira: 20% de R$ 100 é igual a x% de y. Para resolver essa equação, basta multiplicar 20% por R$ 100 e dividir o resultado por 100, já que a porcentagem representa uma fração de 100.
Assim, encontramos que 20% de R$ 100 é igual a R$ 20. Somando esse valor ao preço inicial, temos que o novo preço será de R$ 120.
Portanto, a regra de três é uma ferramenta matemática muito útil para resolver problemas de proporção. Ela pode ser aplicada em diversas situações do nosso cotidiano, auxiliando no cálculo de valores desconhecidos a partir de uma relação proporcional entre três elementos conhecidos.
"Educação é investimento”, diz Lula ao inaugurar curso de matemática no IMPA

Para o presidente Lula, o que faltava no país era oferecer mais oportunidades aos estudantes e “dar a estrutura para que eles se transformem em gênios” - Foto: Ricardo Stuckert/PR
"Educação é investimento”, diz Lula ao inaugurar curso de matemática no IMPA
Compreendendo a dinâmica dos juros compostos: descubra como eles podem impactar os seus investimentos
Compreendendo a dinâmica dos juros compostos: descubra como eles podem impactar os seus investimentos
Os juros compostos têm um papel fundamental no mundo dos investimentos, pois representam a forma como o capital rende ao longo do tempo.
Diferentemente dos juros simples, que são calculados apenas sobre o valor inicialmente investido, os juros compostos são calculados sobre o montante acumulado, permitindo que os ganhos sejam reinvestidos e aumentem progressivamente.
O que são juros compostos?
Os juros compostos são a forma mais comum de remuneração de investimentos financeiros. Basicamente, trata-se de um sistema no qual os rendimentos são incorporados ao montante original, e, posteriormente, são calculados sobre o valor total, incluindo os juros acumulados.
Diferença entre juros simples e compostos:
Para entender melhor a diferença entre juros simples e compostos, vamos imaginar um investimento com uma taxa de 10% ao ano. Se aplicarmos R$1.000,00 com juros simples, no final de um ano, teremos R$1.100,00, ou seja, apenas os R$100,00 de juros em cima do valor inicialmente investido. Porém, com juros compostos, a cada ano, o montante vai aumentando de maneira mais expressiva.
Fórmula dos juros compostos:
A fórmula dos juros compostos é dada por: M = P(1 + i)^n, onde:
- M é o montante acumulado ao final do período;
- P é o principal (valor inicialmente investido);
- i é a taxa de juros em decimal (por exemplo, 10% = 0,10);
- n é o número de períodos que o dinheiro fica investido.
Exemplos de porcentagem de juros compostos:
Para exemplificar o impacto da porcentagem de juros compostos em investimentos, vamos considerar dois cenários hipotéticos:
Exemplo 1:
Uma pessoa investe R$5.000,00 em um título de renda fixa que oferece uma taxa de juros de 8% ao ano, com prazo de resgate de 5 anos. Utilizando a fórmula dos juros compostos, temos:
M = 5000 * (1 + 0,08)^5
M = 5000 * (1,08)^5
M = 5000 * 1,46933
M = R$7.346,65
Portanto, ao final do período de 5 anos, esse investimento renderá aproximadamente R$2.346,65, mostrando a importância dos juros compostos.
Exemplo 2:
Agora, suponha que a mesma pessoa invista os mesmos R$5.000,00, mas com uma taxa de juros de 12% ao ano. Utilizando novamente a fórmula dos juros compostos, temos:
M = 5000 * (1 + 0,12)^5
M = 5000 * (1,12)^5
M = 5000 * 1,76234
M = R$8.811,70
Nesse caso, ao final dos 5 anos, o investimento renderá cerca de R$3.811,70, mostrando como uma pequena variação na taxa de juros pode fazer uma grande diferença no montante acumulado.
Conclusão:
A porcentagem de juros compostos é determinante para entender como os seus investimentos podem evoluir ao longo do tempo. Quanto maior a taxa de juros, maior será a rentabilidade obtida. Portanto, é fundamental analisar cuidadosamente as oportunidades de investimento disponíveis, considerando não apenas a taxa de juros oferecida, mas também o prazo de investimento e os riscos envolvidos. Compreender a dinâmica dos juros compostos pode ser um grande aliado para aumentar seu patrimônio e alcançar seus objetivos financeiros.
A Matemática e criptografia na segurança de informação

Photo by John Schnobrich on Unsplash
A Matemática e criptografia na segurança de informação
A Matemática é uma ciência que tem uma importância crucial na área da criptografia, principalmente quando falamos sobre segurança de informação. A criptografia é o processo de codificar uma mensagem de forma que apenas o destinatário correto possa acessá-la. E é a Matemática que fornece os fundamentos teóricos e algoritmos necessários para tornar a criptografia eficiente e segura.
Um dos principais conceitos matemáticos utilizados na criptografia é a teoria dos números. Ela fornece as bases para a criação de algoritmos de criptografia assimétrica, onde uma chave é usada para criptografar a mensagem e outra para descriptografá-la. Essas chaves são calculadas a partir de operações matemáticas complexas envolvendo números primos, fatoração e função modular.
Além disso, a Matemática também desempenha um papel importante na área da criptoanálise, que é o estudo de quebrar sistemas de criptografia. Para isso, é necessário utilizar métodos matemáticos avançados, como a álgebra linear e a teoria dos grafos, para analisar e encontrar vulnerabilidades nos algoritmos de criptografia.
Outro conceito matemático bastante utilizado na criptografia é a teoria da probabilidade. Ela é usada para avaliar a segurança dos algoritmos de criptografia e calcular a probabilidade de um ataque ser bem-sucedido. Além disso, a probabilidade também é usada na geração de chaves aleatórias, que são essenciais para garantir a segurança dos sistemas criptográficos.
A Matemática também está presente na criptografia de curvas elípticas, uma técnica que utiliza equações matemáticas definidas em um plano para criptografar e descriptografar mensagens. Esse método é amplamente utilizado em dispositivos móveis devido à sua eficiência e segurança. A criptografia de curvas elípticas se baseia em conceitos de geometria algébrica e álgebra abstrata, tornando a Matemática novamente uma peça-chave nesse processo.
Por fim, podemos concluir que a Matemática desempenha um papel fundamental na área da criptografia e na segurança da informação. Ela oferece as ferramentas teóricas necessárias para o desenvolvimento de algoritmos de criptografia robustos e eficientes, bem como na análise e quebra de sistemas criptográficos. Portanto, ao pensar na segurança dos nossos dados e informações, é importante lembrar da importância da Matemática nesse processo.